二叉树中和为某一值的路径
来源:牛客网 JZ24
描述
输入一颗二叉树的根节点和一个整数,按字典序打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
示例1
1
2
|
输入:{10,5,12,4,7},22
返回值:[[10,5,7],[10,12]]
|
示例2
1
2
|
输入:{10,5,12,4,7},15
返回值:[]
|
思路
如下图所示的例子,给定了二叉树与整数22,则可以打印两条路径。第一条10,5,7、第二条10,12;
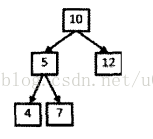
题目中定义路径:从树的根节点开始一直到叶子结点所经过的结点形成一条路径,
也就是说每条满足条件的路径都是以根节点开始,叶子结点结束,如果想得到所有根节点到叶子结点的路径(不一定满足和为某整数的条件),需要遍历整棵树,还要先遍历根节点,所以采用先序遍历;
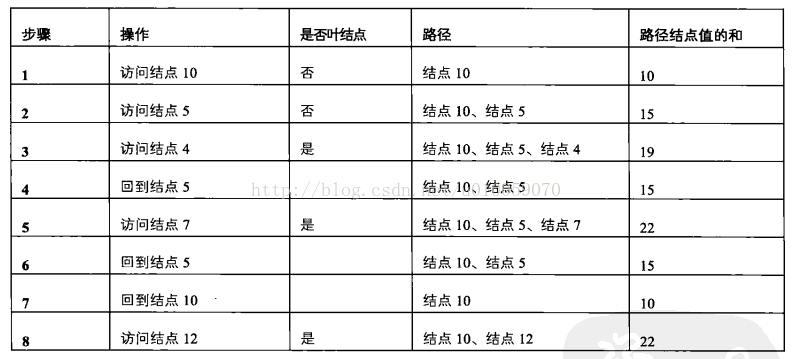
以上的树模拟先序的过程:
10–>5–>4 已近到达叶子结点,不满足要求22,因此该路径访问结束,需要访问下一个路径
因为在访问节点的过程中,我们并不知道该路径是否满足要求,所以我们每访问一个节点就要记录该结点
访问下有一个结点前,要先从结点4退回到结点5,再访问下一个结点7,因为4不在去往7的路径上,所以要在路径中将4删除
10–>5–>7 满足要求,保存该路径
访问下一个结点,从结点7回到结点5再回到结点10
10–>12,满足要求,保存该路径
总结起来就是:
FindPath功能:在给定root子树中,找出合理的路径以达到目标和target
- FindPath实质:二叉树的深度优先遍历 + 每次遍历均判断是否达到条件,若是则输出
- 大致策略
- root入栈,跳入该子树进行寻路操作;
- 若root的这条路径,已满足要求,则将该路径加入到listAll中去;
- 对root左右子树,继续寻路;
- root出栈,该子树访问完毕;
整个流程如下表所示:
1
2
3
4
5
6
7
8
9
10
11
|
// 定义二叉树的结构
public class TreeNode
{
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int x)
{
val = x;
}
}
|
ps: my ugly code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
using System.Collections.Generic;
/*
public class TreeNode
{
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode (int x)
{
val = x;
}
}*/
class Solution
{
public List<List<int>> FindPath(TreeNode root, int expectNumber)
{
// write code here
List<List<int>> list = new List<List<int>>();
List<int> path = new List<int>();
// 如果根节点不为空,那么就遍历树的所有节点查找是否有满足要求的路径
if (root != null)
{
DFS(root, expectNumber, ref list, ref path);
}
return list;
}
private void DFS(TreeNode root, int expectNumber, ref List<List<int>> list, ref List<int> path)
{
// 把当前节点添加进集合
path.Add(root.val);
// 如果当前节点为叶节点, 且和期待值相等,则是把路径加到路径集合中
if (root.left == null && root.right == null)
{
// 这里是因为path元素会随着递归而发生变化,所以存储在路径集合list里时需要开辟新的空间储存路径值再保存
if (expectNumber - root.val == 0)
list.Add(new List<int>(path));
path.Remove(root.val);
return;
}
// 如果当前节点有子节点, 那么递归进入子节点, 传入的期待值必须减去当前节点值
if (root.left != null)
DFS(root.left, expectNumber - root.val, ref list, ref path);
if (root.right != null)
DFS(root.right, expectNumber - root.val, ref list, ref path);
// 当遍历完所有的子节点回到上一级的函数时候,需要把当前的节点移出集合
path.Remove(root.val);
}
}
|
自己本地去构建测试的case, 对正确性做一个验证:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Program
{
static void Main(string[] args)
{
Solution s = new Solution();
TreeNode head = new TreeNode(10);
TreeNode p5 = new TreeNode(5);
TreeNode p12 = new TreeNode(12);
TreeNode p4 = new TreeNode(4);
TreeNode p7 = new TreeNode(7);
head.left = p5;
head.right = p12;
p5.left = p4;
p5.right = p7;
var res = s.FindPath(head, 22);
foreach (var item in res)
{
foreach (var ele in item)
{
Console.WriteLine(ele);
}
Console.WriteLine("**********split line*********");
}
}
}
|
总而言之, 就是, 当用前序遍历的方式访问到某一节点时,我们把该节点添加到路径上,并累加该节点的值。如果该节点为叶节点,并且路径中节点值的和刚刚好等于输入的整数,则当前路径符合要求,然后打印该路径。如果当前节点不是叶节点,那么继续访问它的子节点。当前节点访问结束之后,递归函数将自动回到它的父节点。因此,我们在函数退出之前需要在路径上删除当前节点并减去当前节点的值,以确保返回父节点时路径刚好是从根节点到父节点。
测试用例
- 功能测试(可尝试构造多个树的case, 和固定值)
- 特殊输入的测试 (一些临界值和极端的case情况)
本题考点
- 考察二叉树的理解和编程能力;
- 考察对二叉树遍历,查找和递归相互关联的概念和理解;
高手解法与赏析
思路:
1、采用深度优先搜索的方式,枚举每一条从根节点到叶子节点的路径。当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径。
2、我们也可以采用广度优先搜索的方式,遍历这棵树。当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径。为了节省空间,我们使用哈希表记录树中的每一个节点的父节点。每次找到一个满足条件的节点,我们就从该节点出发不断向父节点迭代,即可还原出从根节点到当前节点的路径。
举本例说明:
-
采用深度优先搜索的方式:
-
二叉树:{10,5,12,4,7}, 目标值:22
-
根据二叉树可以枚举出所有从根节点到叶子节点的路径【10,5,4】、【10,5,7】、【10,12】
-
将不同的路径节点值相加,并判断符合结果等于目标值的路径:【10,5,7】、【10,12】
-
图表题解:
| 步骤 |
二叉树序列 |
目标值 |
路径列表 |
返回路径集合 |
| 1 |
{10,5,12,4,7} |
22 |
【10】 |
|
| 2 |
根左子树{5,4,7} |
12 |
【10,5】 |
|
| 3 |
左子树{4} |
7 |
【10,5,4】 |
|
| 4 |
右子树{7} |
7 |
【10,5,7】 |
【【10,5,7】】 |
| 5 |
根右子树{12} |
12 |
【10,12】 |
【【10,5,7】,【10,12】】 |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
import java.util.ArrayList;
import java.util.LinkedList;
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
//初始化集合
ArrayList res = new ArrayList<>();
LinkedListpath = new LinkedList<>();
public ArrayList FindPath(TreeNode root,int target) {
dfs(root, target);
return res;
}
public void dfs(TreeNode root,int tar){
if(root == null){
return;
}
//将root节点放入路径集合
path.add(root.val);
//更新目标值,每放入一个节点,目标值应该相应减去对应节点的值,直到目标值为0
tar -= root.val;
//如果目标值减到了0 && 左节点为空 && 右节点为空 证明树已遍历完,此路径为目标路径
if(tar==0 && root.left == null && root.right == null){
res.add(new ArrayList(path));
}
// 递归左右子树
dfs(root.left, tar);
dfs(root.right, tar);
//删除当前节点,在回溯过程中,此节点不在新路径上
path.removeLast();
}
}
|

