旋转数组的最小数字
来源:牛客网 - JZ6 旋转数组的最小数字
描述
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
示例1
思路
(1) 我的想法是类似二分查找法, 用两个指针分别指向数组的第一个元素和最后一个元素。(这个解法来自于剑指Offer 2.3节习题解法)
(2) 接着我们可以找到数组中间的元素:
如果该中间元素位于前面的递增子数组,那么它应该大于或者等于第一个指针指向的元素。此时数组中最小的元素应该位于该中间元素的后面。我们可以把第一个指针指向该中间元素,这样可以缩小寻找的范围。移动之后的第一个指针仍然位于前面的递增子数组之中。如果中间元素位于后面的递增子数组,那么它应该小于或者等于第二个指针指向的元素。此时该数组中最小的元素应该位于该中间元素的前面。
(3) 接下来我们再用更新之后的两个指针,重复做新一轮的查找。
按照上述的思路,第一个指针总是指向前面递增数组的元素,而第二个指针总是指向后面递增数组的元素。最终第一个指针将指向前面子数组的最后一个元素,而第二个指针会指向后面子数组的第一个元素。也就是它们最终会指向两个相邻的元素,而第二个指针指向的刚好是最小的元素。这就是循环结束的条件。
以题目所给的数组{3,4,5,1,2}为例,下图展示了在该数组中查找最小值的过程:
ps: my ugly code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
package main
import "fmt"
func minNumberInRotateArray(rotateArray []int) int {
// write code here
if len(rotateArray) == 0 {
return 0
}
left := 0
right := len(rotateArray) - 1
middle := left
for rotateArray[left] >= rotateArray[right] {
if right-left == 1 {
middle = right
break
}
middle = (left + right) >> 1
// 特殊情况: 如果下标left, right和mid指向的三个数字相等, 则只能顺序查找
if rotateArray[left] == rotateArray[middle] && rotateArray[middle] == rotateArray[right] {
return getMinInOrder(rotateArray, left, right)
}
// 缩小查找范围
if rotateArray[middle] >= rotateArray[left] {
left = middle
} else if rotateArray[middle] <= rotateArray[right] {
right = middle
}
}
return rotateArray[middle]
}
func getMinInOrder(numbers []int, left int, right int) int {
result := numbers[left]
for i := left + 1; i <= right; i++ {
if numbers[i] < result {
result = numbers[i]
}
}
return result
}
func main() {
var nums1 = []int{3, 4, 5, 1, 2}
var nums2 = []int{4, 3}
var nums = []int{1, 2, 2, 2, 2, 2}
fmt.Println(minNumberInRotateArray(nums1))
fmt.Println(minNumberInRotateArray(nums2))
fmt.Println(minNumberInRotateArray(nums))
}
|
这里需要注意的是:
(1)把middle初始化为left的原因:一旦发现数组中第一个数字小于最后一个数字,表明该数组是排序的,就可以直接返回第一个数字了。
(2)特殊情况的分析:如果下标为left、right和middle指向的三个数字相等,则只能顺序查找,因此这里定义了一个GetMinInOrder()方法。
测试用例
- 功能测试(输入的数组是升序排序数组的一个旋转,数组中有重复数字或者没有重复数字)
- 边界值测试 (输入的数组是一个升序排序的数组,只包含一个数字的数组)
- 特殊输入的测试(输入NULL指针)
本题考点
- 考察二分查找的理解和编程能力;
- 考察沟通学习的能力,短时间内接触“数组旋转”的概念,理解并学习到;
- 考察思维的全面性。对于数组中有相同数字的特例,是否考虑到并得到很好地处理;
高手解法与赏析
二分查找
这种二分查找难就难在,arr[mid]跟谁比.
我们的目的是:当进行一次比较时,一定能够确定答案在mid的某一侧。一次比较为 arr[mid]跟谁比的问题。
一般的比较原则有:
- 如果有目标值target,那么直接让arr[mid] 和 target 比较即可。
- 如果没有目标值,一般可以考虑 端点
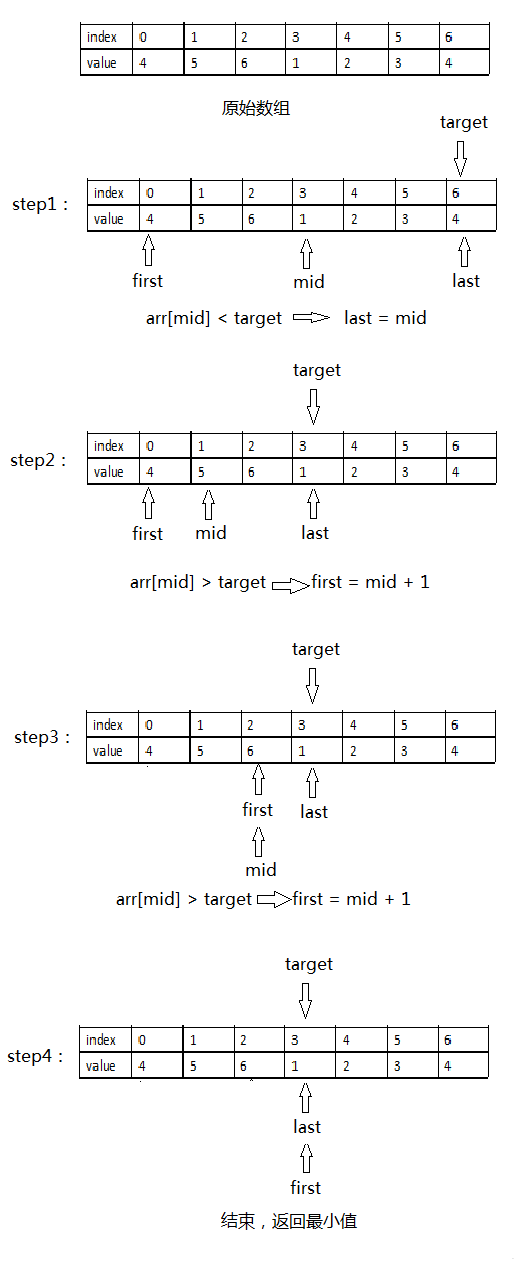
这里我们把target 看作是右端点,来进行分析,那就要分析以下三种情况,看是否可以达到上述的目标。
-
情况1,
1
|
arr[mid] > target:4 5 6 1 2 3
|
- arr[mid] 为 6, target为右端点 3,
arr[mid] > target, 说明[first … mid] 都是 >= target 的,因为原始数组是非递减,所以可以确定答案为 [mid+1…last]区间,所以 first = mid + 1
-
情况2,
1
|
arr[mid] < target:5 6 1 2 3 4
|
- arr[mid] 为 1, target为右端点 4,
arr[mid] < target, 说明答案肯定不在[mid+1…last],但是arr[mid] 有可能是答案,所以答案在[first, mid]区间,所以last = mid;
-
情况3,
- 如果是 1 0 1 1 1, arr[mid] = target = 1, 显然答案在左边
- 如果是 1 1 1 0 1, arr[mid] = target = 1, 显然答案在右边
所以这种情况,不能确定答案在左边还是右边,那么就让last = last - 1;慢慢缩少区间,同时也不会错过答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
// c++
class Solution {
public:
int minNumberInRotateArray(vector<int> rotateArray) {
if (rotateArray.size() == 0) return 0;
int first = 0, last = rotateArray.size() - 1;
while (first < last) { // 最后剩下一个元素,即为答案
if (rotateArray[first] < rotateArray[last]) { // 提前退出
return rotateArray[first];
}
int mid = first + ((last - first) >> 1);
if (rotateArray[mid] > rotateArray[last]) { // 情况1
first = mid + 1;
}
else if (rotateArray[mid] < rotateArray[last]) { //情况2
last = mid;
}
else { // 情况3
--last;
}
}
return rotateArray[first];
}
};
|
参考资料
牛客网精华题解
Edison Zhou 题解

